Do bicycle hubs hang from the spokes above or do they stand on the spokes below?
This question is occasionally debated on forums and other places in the cycling world, where impassioned people come together to defend their side of the argument – sometimes even using the same understanding of how a bicycle wheel works to draw completely different conclusions. In this article we’re going to look at the arguments for both theories in detail, and then use current scientific understanding of this topic to explain why the answer may not be as straight forward as it first appears.

All wheels consist of a rim, hub, and spokes. The rim is the outside edge of the wheel, over which a tire is usually mounted. The hub is the center of the wheel, which usually contains bearings to reduce the friction between the hub and an axle. The hub and rim are usually connected with spokes, which can vary in size, shape, and number.
Original Image by jim hatch on Unsplash
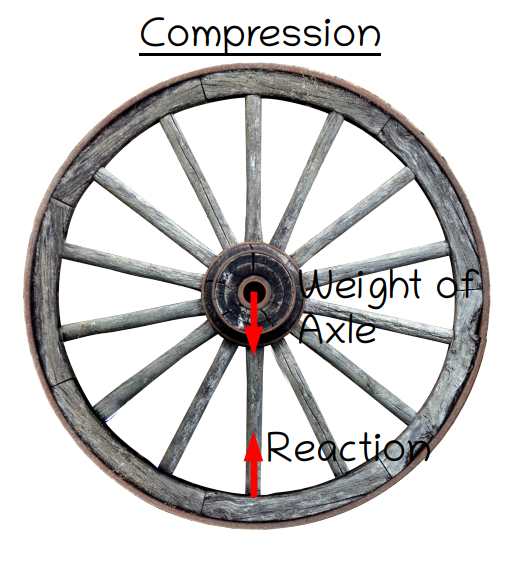
In most wheels, the spokes are relatively thick and heavy, but bicycle wheels are special because their spokes are made of thin wires which are tightened, or pre-tensioned as the wheel is built. Let’s consider the advantages of this by comparing the construction of a bicycle wheel with that of a traditional wagon wheel.
The wooden spokes of a typical wagon wheel are made of wood and are very good at carrying compressive, or pushing forces. Not only is wood fundamentally good at resisting compression, but the fact that the spokes are relatively thick prevents them from buckling, or bending out to the side under load. The way the spokes connect to the hub and rim, by simply slotting into pre-drilled holes, also optimizes the wheel to resist compressive loads.
Original Image by maya7777 on Pixabay
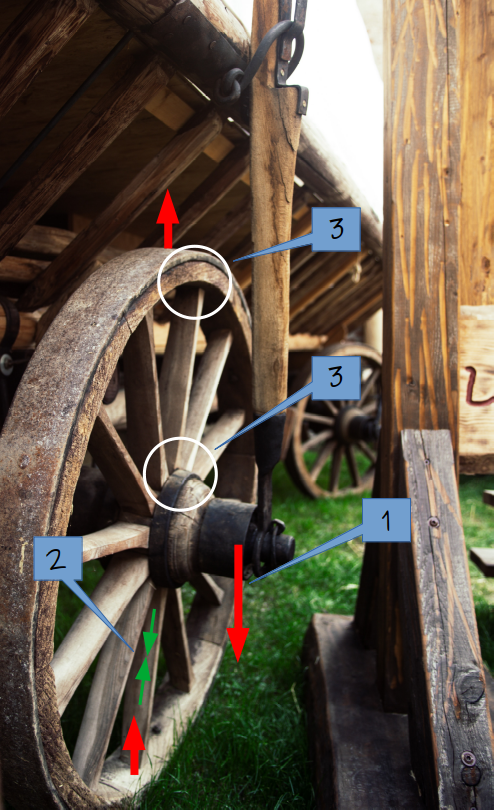
When a wagon wheel is loaded, gravity pulls the hub down (1), which compresses the spokes below (2), forcing them into the bottom of their corresponding holes and holding the joints between the hub, rim, and lower spokes tightly together. At the same time, the hub also pulls down on the spokes above, but in this case the downward force acts to pull the joints between the hub, spokes and rim apart, breaking the direct connection between the spokes the bottoms of the holes (3).
This is why wagon wheel hubs unquestionably stand on the spokes below the hub: when gravity forces these spokes into the bottom their corresponding holes, a strong and direct connection is made whose strength is only limited by the strength of the wood itself, whereas the strength of the connections above the hub is limited by friction, which significantly decreases the contribution of the spokes above to the strength of the wheel.
Original Image by camilo jimanez on Unsplash
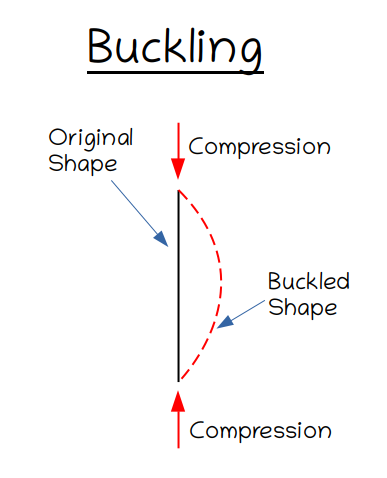
Bicycle spokes, on the other hand, are very thin and not able to resist compressive forces very well. You can experience this for yourself by pushing on the ends of a spoke, coat hanger or other similar thin piece of metal and observing what happens. It doesn’t take very much force to cause the spoke to bend outwards to the side – a phenomenon called buckling, which is most likely in slender, flexible objects.
In order to keep this from happening, bicycle spokes are pre-tensioned by tightening them. The tension in the spokes holds them perfectly straight, and as long as even a small amount of tension is present they will be prevented from buckling. The pre-tension in the spokes also increases the robustness of the wheel, because it allows the rim to flex as the wheel turns – and the higher the pre-tension in the spokes, the more the rim can flex before the spokes slacken and the wheel loses its shape.

The fact that all of the spokes are designed to always be in tension is the basis for the argument that the hub hangs from the spokes. By definition, if a spoke is in tension, it cannot be in compression at the same time, and if a spoke isn’t in compression, it can’t be transferring a compressive force – this means that under normal conditions, neither the hub nor the rim will ever experience the spokes pushing on them, no matter how the wheel is turned or loaded. The spokes can even be replaced by high-strength threads, which are flexible and therefore incapable of being in compression, and the wheel will perform the exact same way.
Public Domain Image from Wikimedia Commons

If the explanation above is too theoretical, this can also be understood intuitively by imagining an exercise band. When you pull up on an exercise band, you feel the band resisting and trying to pull your hands back down because the tension is increasing. Now if you slowly move your hands back down, the tension in exercise band obviously decreases, but at no point will you feel the exercise band pushing back up on your hand – it continues to pull down on your hands until it slackens, at which point it simply loses its shape.
This is exactly what happens with bicycle spoke: the initial tension in the exercise band is equivalent to the pre-tension in the spokes, and you moving your hands down is equivalent to the rim flexing beneath the spokes. As the rim continues to flex, the tension in the spokes continues to decrease until they slacken, at which point they either buckle or simply unseat from the rim, losing the ability to transfer forces completely. As with the exercise band, the spokes always pull on the rim, never push, clearly demonstrating that no compressive forces are transferred.
Original Image by Fausto Sandoval on Unsplash
So why does the argument that the hub stands on the spokes below persist? The leap that has to be made here is understanding that the spokes below the hub are essential to the behavior of the wheel, despite the fact that they cannot carry real compressive forces. Luckily for us and contrary to what is often said on the internet, the way a bicycle wheel works is actually rather well understood. Scientists and engineers have not only described their behavior analytically, using physical principles and mathematical equations, but also verified their theories through computer models and physical tests carried out on real bicycle wheels. This allows us to move beyond mere speculation and actually analyze what actually happens when a bicycle wheel is loaded.
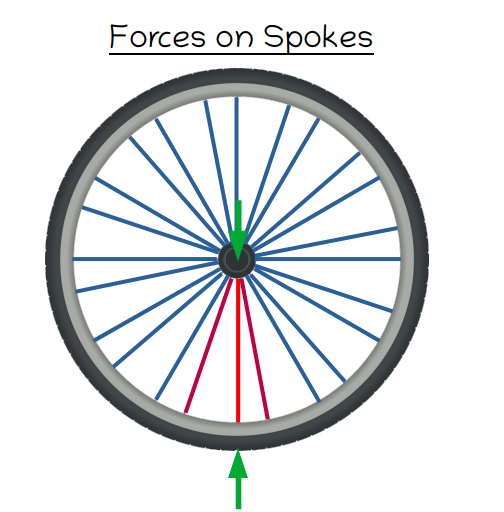
In short, when a bicycle wheel rolls across the ground, a flat spot develops in the rim just above the ground, because the ground causes the rim to bend. This logically causes the tension in the spokes above to decrease because the rim flexes upwards, but at the same time the tension in the other spokes slightly increases*. A relatively easy-to-understand analysis of a computer model which demonstrates this behavior can be found here, and although I disagree with some of the author’s semantics I believe the physics to be correct, and their model also agrees with all of the published literature I have read on the topic.
Red = Decrease in Tenson
Blue = Increase in Tension
Once the forces that develop within a bicycle wheel are known it is trivial to understand the way each individual component of a wheel contributes to its behavior, because the ‘amount’ that each individual component contributes to the carrying capacity of the wheel is directly proportional to how much the force within that component changes. In our case, the computer model shows that the tension changes significantly in the spokes directly above the ground, but hardly changes at all in any of the spokes further away from the ground. This implies that the spokes just above the ground are most active in carrying the load on the wheel, despite the fact that they remain in tension.
This is the hardest part of the behavior of a bicycle wheel to understand, so I will attempt to do so using a few analogies. Even though the spokes just above the ground are always in tension, which means that they can’t physically push on the hub and rim and transfer compression, it can be stated mathematically that the compression in these spokes has increased.

This is similar to saying that subtracting a negative number is the same thing as addition – if I have two oranges, and I take away negative two oranges, what happens? Obviously 2- (-2) = 4 oranges, but negative oranges don’t actually exist, so I am using a physically nonsensical mathematical concept to come up with a real and valid answer. In our case, this essentially implies that a decrease in tension can be represented as an increase in compression, even though a pushing force is never physically felt.
Two tangerines for chinese new year by ProjectManhatten, available
under a Creative Commons Attribution-ShareAlike 3.0 Unported license.

Another way to think about this is to imagine a kitchen scale. If you tare a scale and then place 1kg of potatoes on it, the scale will read 1kg – but if you retare the scale after adding the potatoes, the scale reads zero even though the potatoes still weigh 1kg. If you then remove some potatoes, the scale reads a negative number, even though the remaining potatoes clearly don’t have a negative weight – the negative number is a mathematical construct which simply indicates that weight has been removed compared to when the scale was tared.
Original Image from on Pxfuel
This can also be done with a bicycle wheel by simply setting the pre-tension in the wheel as the new zero-point, which is equivalent to taring the scale after the potatoes have been added. This results in any decrease in tension mathematically appearing as compression, despite the fact that this decrease is not physically felt as a pushing force. The relative change in tension can be measured no matter what you choose as the zero-point, but sometimes the absolute tension appears as a positive number and sometimes a negative number. This is a perfectly valid mathematical operation which is called the ‘principle of superposition’ in engineering and which is often performed in basic structural analysis.
The other key thing to understand, which I think is often poorly explained, is that the analysis of how a bicycle wheel works doesn’t lead to the conclusion that the entire weight of the bicycle is being transferred through the spokes between the hub and the ground. Instead, it indisputably shows that all spokes are active in transferring the load – the decrease in tension in the spokes below the hub is simply being counteracted by an increase in the tension of the other spokes. This makes sense, because all of the forces on the wheel need to balance each other out in order to maintain equilibrium. If equilibrium is broken, it is implied that either different parts of the wheel are accelerating away from each other, so order for all parts of the wheel to remain connected, the tension in the spokes below the hub must decrease to maintain equilibrium, and the tension in the remaining spokes must increase for the same reason. The fact that the tension only increases slightly in the spokes away from the ground doesn’t mean that those spokes are unimportant, it simply means that only a small increase is necessary to balance out the other forces present within the wheel because there are so many spokes contributing to this effect. At the end of the day, the tension in the spokes must balance the force imposed on the hub through the axle, and it turns out that to achieve this the tension in the spokes below the hub decreases significantly while the tension everywhere else increases slightly.

A thought experiment which often arises in discussions about this topic is: would cutting the spokes above or below the hub have a greater effect on the wheel? The counter-intuitive result of this analysis is that an individual spoke between the hub and the ground is indeed more significantly involved with transferring the load of the bicycle, because its tension changes much more than the tension in any one spoke above the hub. However, the wheel definitely wouldn’t fail catastrophically if the spoke below the hub were cut – instead, the forces would simply redistribute in order to maintain equilibrium, implying that the tension in the next-closest spoke would immediately decrease to balance the weight of the hub and the tension in the remaining spokes.
Original Image by twin1961 on Pixabay
The effect of cutting one or two spokes would be relatively minor, but if more spokes were cut the way the forces transfer through the wheel would fundamentally start to change. The rim would still bend around the point of ground contact, but because it is the bending of the rim that causes the tension in the spokes above to change, the tension in the spokes closest to this point would eventually stop decreasing because the remaining spokes would be so far away from the ground that the bending of the rim would have little effect on them. In addition, if all of the spokes in the lower half of the wheel were cut, the remaining spokes would be angled downward in which case their tension would increase significantly simply because the hub would be pulling down on them due to gravity.
If, on the other hand, spokes above the hub were cut, the opposite effect would occur – the tension in the next-closest spokes would increase, while the tension spokes below the hub would decrease to maintain equilibrium. The answer to the question ‘Would cutting the spokes above or below the hub be more significant?’ is that it depends. In both cases, the force distribution within the wheel would change, eventually to the point that the wheel would no longer be acting as a pre-tensioned structure. I suspect that if the spokes below the hub were cut, a stationary wheel could probably resist the weight of the bicycle with even just a single spoke above the hub, but if the spokes above were cut, the tension in the spokes below would eventually decrease to the point of actually being in compression, at which point they would buckle. Therefore, my opinion is that the spokes below the hub are the most important for resisting the forces imposed on the wheel, but more lower spokes could be cut before the wheel fails catastrophically.
The overall conclusion of this analysis is that the wheel acts as a system, where each individual component has a role to play. The hub doesn’t hang from the rim, because the force in the spokes below the hub changes much more than the force in the spokes above as the wheel turns. The hub doesn’t stand on the spokes either though, because even though these spokes are more active in resisting the load on the wheel, they require the other spokes to balance the forces and maintain equilibrium. Although all of the spokes are always in tension, because they would buckle if they weren’t, a decrease in tension can mathematically be represented as compression, even if this is physically nonsensical. And finally, if any one spoke were cut, the wheel wouldn’t immediately fail catastrophically, but the distribution of forces within the wheel would change until enough spokes were cut to fundamentally alter the way the wheel worked as a system.
References
- https://www.quora.com/When-riding-a-bicycle-are-you-suspended-from-the-rim-by-the-spokes-between-the-hub-rim-at-the-tallest-point-of-the-wheel-or-are-you-supported-by-the-spokes-between-the-hub-the-rim-pushing-against-the-rim-tyre-at-the-lowest-point
- http://hea-www.harvard.edu/~fine/opinions/bikewheel.html
- https://www.astounding.org.uk/ian/wheel/index.html
- Burgoyne, C. J., and R. Dilmaghanian. “Bicycle wheel as prestressed structure.” Journal of Engineering Mechanics 119.3 (1993): 439-455.
- Papadopoulos, Jim M. “Bicycle wheel as prestressed structure.” Journal of Engineering Mechanics 121.7 (1995): 847-849.
- Brandt, Jobst. The Bicycle Wheel. 3rd ed., Palo Alto, California, Avocet, 1993.
- Pippard, AJ Sutton, and W. E. Francis. “XX. On a theoretical and experimental investigation of the stresses in a radially spoked wire wheel under loads applied to the rim.” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 11.69 (1931): 233-285.
- Ford, Matthew. Reinventing the wheel: Stress analysis, stability, and optimization of the bicycle wheel. Diss. Northwestern University, 2018.
*I’m not sure exactly what the physical mechanism is that distributes forces to the spokes away from the ground, but the finite element analysis I linked to here provides a clue by showing that the tension in the rim increases slightly as the wheel is loaded. This suggests that the increase in tension is at least partially due to arch action, which basically converts a vertical force to a horizontal one, allowing a vertical force on the rim to be distributed to the spokes horizontally. I suspect that the remainder is simply due to gravity pulling the hub down, which doesn’t contradict the fact that the lower spokes are most active when the wheel is loaded. Gravity does increase the tension on some of the spokes, but this is overshadowed by the effect of the bending rim on the spokes below the hub.